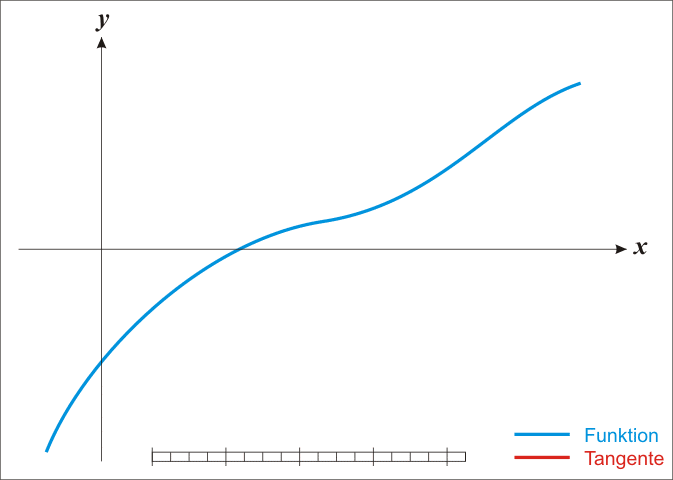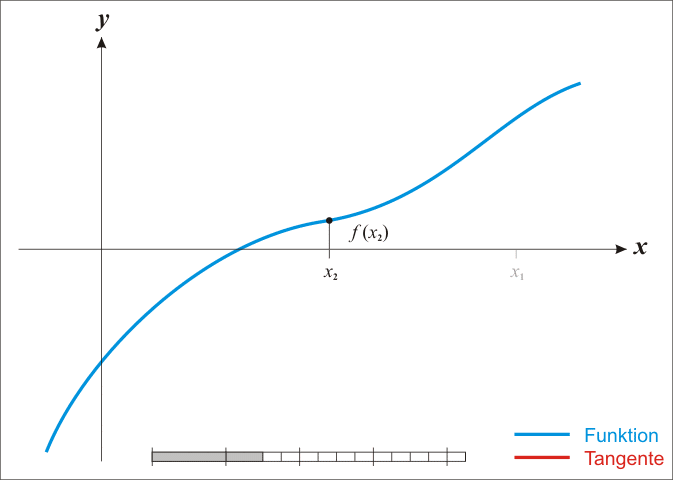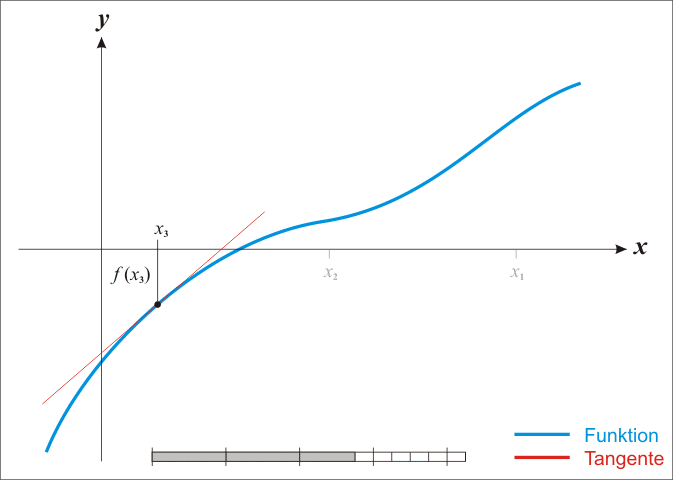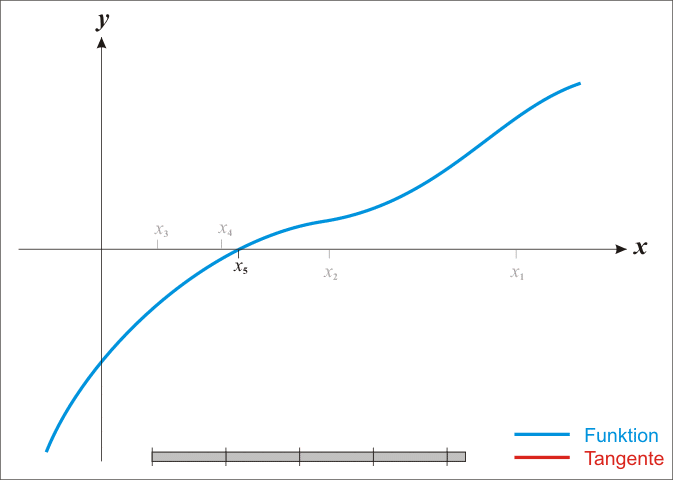
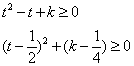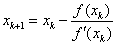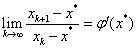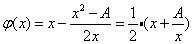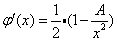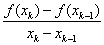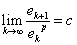本文将从一道经典的面试题说起：实现平方根函数，不得调用其它库函数。

函数原型声明例如以下：

double Sqrt(double A);

二分法

二分法的概念

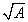
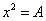
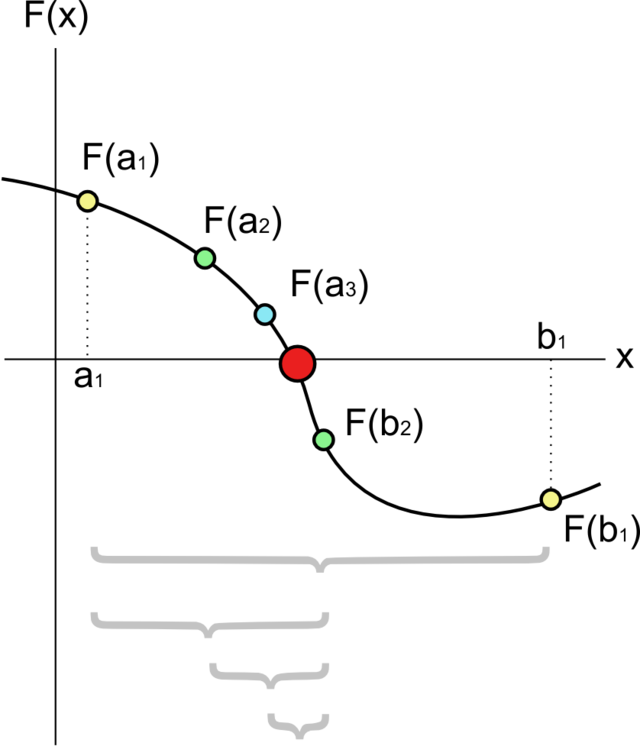
求，等价于求方程的非负根（解）。求解方程近似根的方法中，最直观、最简单的方法是二分法。“二分法”算法过程例如以下：

1. 先找出一个区间 [a, b]，使得f(a)与f(b)异号。
2. 求该区间的中点 m = (a+b)/2，并求出 f(m) 的值。
3. 若 f(m) * f(a) < 0 则取 [a, m] 为新的区间, 否则取 [m, b].
4. 反复第2和第3步至理想准确度为止。

二分法的过程可用下图表示：

初始区间的选定

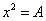
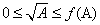
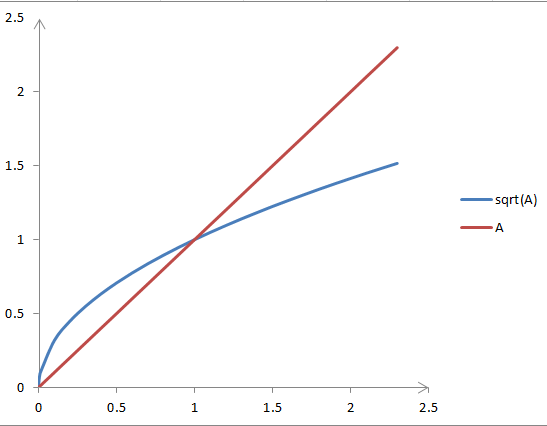
可见，若要用“二分法”求方程，首先要找到一个区间 [a, b]，使得f(a)，f(b)异号。a能够取0，这非常easy想到；但b怎样选取，即怎样选取b=f(A)，使得？

取f(A)=A？不行，由于它不能始终保证：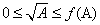

从图像可知，当A>1时，才有。若用A作为第一步的上界，则在A小于1时，将无法得到正确结果。

同一时候可知，sqrt(A)在原点处的切线平行于y轴，所以找不到常数项为零的多项式f(A)，使得。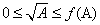

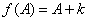
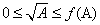
据此，可推出一个，使得成立。

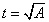
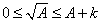
令，则t>=0，， 等价于，即

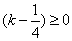
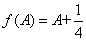
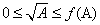
显然，当时，上式成立，所以k能够取[1/4, +∞)的随意值，最好还是取k=1/4，即有

，使得成立。

二分法的误差

为了说明二分法的误差，须要借助一个定理。

零点定理：若f(x)在(a,b)连续，且f(a)f(b)<0，则f(0)在(a, b)内有零点。

二分法每次迭代都可以保证实际解在区间[a, b]范围内，所以每次迭代的误差都小于当前区间的宽度，这也是迭代的结束条件（通常误差给定）。

二分法实现sqrt

依据以上分析，能够非常快写出sqrt的“二分法”版本号：

double Sqrt(double A){	double a = 0.0, b = A + 0.25, m; // b = A 是错误的上界		// while(b - a > 2*DBL_EPSILON) { // sometimes dead cycle when m==a or m==b.	for(;;) {		m = (b + a)/2;		if( m-a < DBL_EPSILON || b-m < DBL_EPSILON ) break; 		if( (m*m - A) * (a*a - A) < 0 ) b = m;		else a = m;	}	return m;}

须要注意的是：

• 初始上界是A+0.25，而不是A；
• double型的精度DBL_EPSILON，不能任意指定；

牛顿迭代法

以下介绍还有一种应用广泛的方法——牛顿迭代法。

牛顿法的概念

牛顿迭代法是迭代法的一种，它的迭代格式为：

 

牛顿法具有明显的几何意义，x[k+1]正是曲线在x[k]处的切线与x轴的交点的横坐标。因此，牛顿法也称切线法。

来自Wikipedia的一个动态图非常好的解释了这样的几何意义：

牛顿法初值的选定

在開始牛顿迭代法之前，须要选定一个d迭代初值x0。依据前文分析，求sqrt(A)，也能够取x0 = A+0.25；

牛顿法sqrt

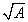
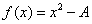
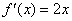
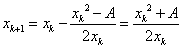
依据牛顿法，求即求的非负根，，

所以，此时的牛顿递推式为：

 

离实现牛顿法还差关键一步：迭代的结束条件。

在不知道误差公式，且要求误差尽可能小情况下能够使用还有一种方法——限定f(x)=0的误差（此法仅限于不给误差范围，且要求误差尽可能小时使用）。

据此，实现的sqrt例如以下：

double Sqrt(double A){	double x0 = A + 0.25, x1, xx = x0;	for(;;) {		x1 = (x0*x0 + A) / (2*x0);		if(fabs(x1 - x0) <= DBL_EPSILON) break;		if(xx == x1) break; // to break two value cycle.		xx = x0;		x0 = x1;	}	return x1;}

这段程序里的while条件是fabs(x1*x1-A) > 5*DBL_EPSILON是由于，x的误差在2*DBL_EPSILON范围内，所以x*x的误差就在4*DBL_EPSILON范围，考虑到浮点乘法的精度丢失，所以为5*DBL_EPSILON。

迭代法的理论基础

迭代格式收敛的前提

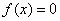
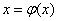
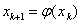
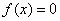
迭代法在进行“迭代”之前，需将原方程改写成的形式；再用迭代格式，逐次逼近的实际解x*。

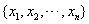
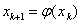
整个过程的全部x构成了数列：（迭代序列），数列的递推式即；

所以，迭代法可以求得近似解的前提是

         

当中x*为方程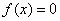的实际解。

迭代格式收敛的条件

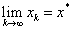
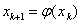
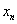
迭代法收敛的前提是 ，这非常好理解；但要用此式验证迭代式是否收敛，必须先通过递推式求出通项；

是否有更简单的方法判定迭代格式收敛？当然有，以下介绍一个定理可以简便的判定迭代格式是否收敛，同一时候也能判定误差。

---

定理  迭代格式收敛条件（Vipschitz条件）

若迭代函数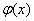满足：

①一阶导数连续；

②当x∈[a, b]时，有；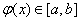

③存在常数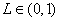，使得；

则

1. 方程有唯一根x*；
2. 对随意x0∈[a, b]，迭代格式收敛，且；
3. ，（事后误差预计）；
4. ，（事前误差预计）；
5. 

---

定理应用

以下以求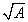的近似解为例，说明定理怎样用：

1）推断收敛

相应的迭代函数为：

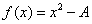
它的导函数为：

在[0, A+0.25]区间内它显然连续，且存在L=1/2使得；；即满足收敛的三个条件；

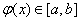
2）预计误差（迭代次数）

有了L = 1/2；就能够依据定理估算：

①给定误差情况下，须要迭代几次？

②给定迭代次数，终于近似解的误差？

比方，如果题目要求的精度是：小数点后2位（精确到0.01），那么误差要小于0.01 / 2 = 0.005；仅仅需依据初值x0和第一次迭代结果x1和定理的结论4，便可算出迭代次数k，这里不再罗列（公式编辑起来比較麻烦）。

相同，依据x0，x1和结论4，也能够非常方便的算出第k次迭代的误差；

推广——一般方程求近似解

本文指出的二分法、牛顿迭代法是求解方程近似解的常见方法，不只限于求sqrt，但在本文所实现的sqrt程序的基础上，能够非常快实现求解其它方程的程序。

二分法

比方，例如以下程序段就是二分法求解随意方程f(x)=0的程序：

double bisection(double (*f)(double), double a, double b, double eps){	double m;	assert( f != NULL && f(a) * f(b) < 0.0 && (b-a) > DBL_EPSILON); // (b-a) > DBL_EPSILON 即 b > a	while( b - a > eps ) {		m = (a + b)/2;		if( f(m) * f(a) < 0.0 ) b = m;		else a = m;	}	return m;}

这个程序较为“好用”，仅仅需给出函数f，区间[a, b]，误差eps就可以。

迭代法

相同，有了对迭代法的理论基础，我们知道了迭代法的误差怎样预计。以下是迭代法求一般方程的近似解的程序：

double iteration(double (*g)(double), double L, double x0, double eps){	double x1, t = L/(1 - L);;	for(;;) {		x1 = g(x0);		if(fabs( t*(x1-x0) ) < eps) 			break;		x0 = x1;	}	return x1;}

这个函数没有上面的二分法那么好用，由于须要依据f(x)自行推出递推函数g，并依据递推函数的倒数找到一个常数L；再给出初值x0，误差eps。

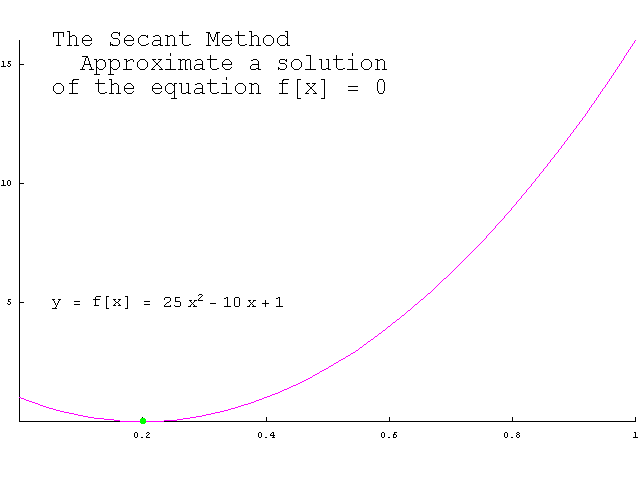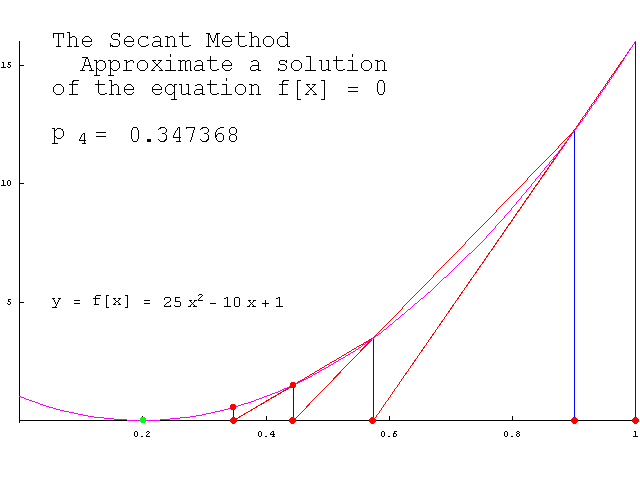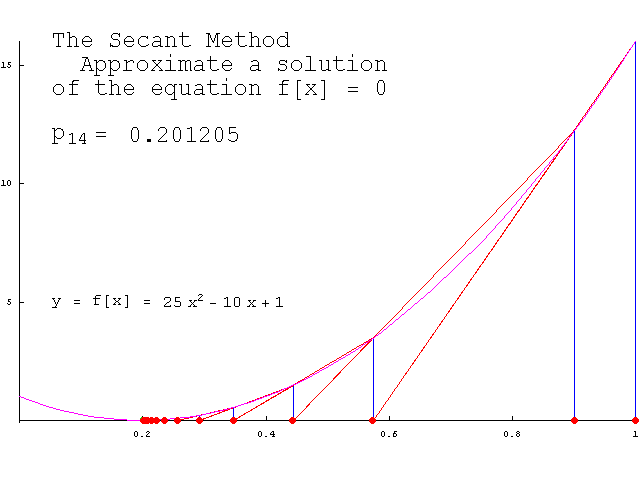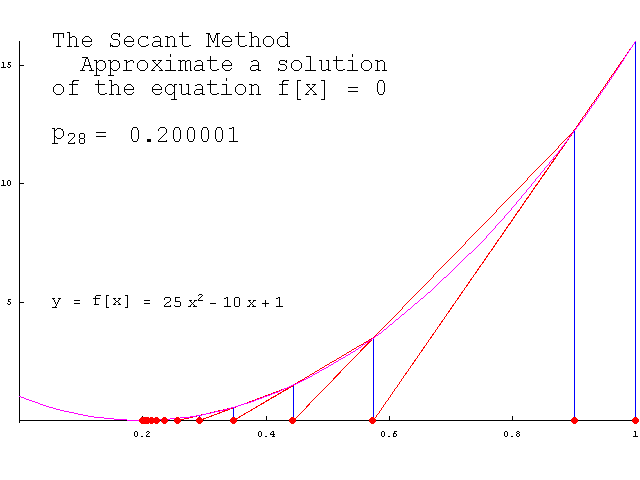
割线法

其实，真正通用的牛顿法非常难实现，由于从f(x)推出它的导函数f1(x)的过程并不easy。割线法能够避免这一难题，它使用差商：

来取代牛顿公式中的导数f'(xk)，于是得到了“割线法”迭代公式：

割线法和牛顿法类似，有着明白的几何意义。以下的gif动态地展示了割线法的几何意义（若没有看到动画效果可尝试刷新本页）：

（图片来自，）

割线法求一般方程的近似解的程序例如以下：

double secant(double (*f)(double), double x0, double x1, double eps){	double x2;	for(;;) {		x2 = x1 - f(x1)/(f(x1) - f(x0))*(x1 - x0);		if( fabs(x2-x1) < eps ) 			break;		x0 = x1;		x1 = x2;	}	return x2;}

这个函数也非常好使用，仅仅需给出f，[a, b]，eps就可以。

割线法实现的sqrt例如以下：

double Sqrt(double A){	double x0 = 0, x1 = A+0.25, x2;	double fx0 = x0*x0 - A, fx1 = x1*x1 - A;		for(;;) {		x2 = x1 - fx1*(x1-x0) / (fx1-fx0);		if(fabs(x2 - x1) < 2*DBL_EPSILON)			break;		x0 = x1; fx0 = fx1; 		x1 = x2; fx1 = x2*x2 - A;	}	return x2;}

收敛速度对照

对于sqrt的实现，本文介绍了三种方法，分别为：二分法，牛顿法，割线法；

二分法的收敛速度

对于二分法，相邻两次的误差ek+1和ek间的关系为：

，

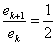
由此，我们能够引申出迭代法收敛速度的判定标准：

---

定义  迭代法收敛的阶

设序列{xk}收敛于x*，并记ek = xk - x*，假设存在非负常数c和正常数p，使得

则称序列{xk}是p阶收敛的。当p=1，且0<|c|<1时，称为线性收敛；当p>1时，称超线性收敛，特别是p=2时，称平方收敛。

---

由收敛阶的定义可知，二分法是线性收敛的。

牛顿法的收敛速度

要确定牛顿法收敛的阶，须要经过一番推导，限于篇幅，这里直接给出结论：

当x*是f(x)=0的单根（回想一下二次方程）时，牛顿法至少是二阶收敛的；

当x*是f(x)=0的重根时，牛顿法至少是一阶收敛的。

割线法的收敛速度

分析割线法收敛的阶相同不易，它比牛顿法略慢一些；有知道的同学能够告诉我；

实验对照

以下通过实验对照几种方法的收敛速度。实验以不同版本号的sqrt求出终于值所用的迭代次数为收敛速度的标准。

实验程序例如以下：

#include 
      
        // for fabs sqrt#include 
       
         // for DBL_EPSILON DBL_DIG etc.#include 
        
          // for clock#include 
         
          #include 
          
           int iterateCount = 0;double BisectionSqrt(double A){	double a = 0.0, b = A + 0.25, m;		for(;;){		m = (b + a)/2;		++iterateCount; // count iterate.		// printf("  %.15f\n", m);		if( m-a < DBL_EPSILON || b-m < DBL_EPSILON ) break; 		if( (m*m - A) * (a*a - A) < 0.0 ) b = m;		else a = m;	}	return m;}double NewtonSqrt(double A){	double x0 = A + 0.25, x1, xx;	for(;;) {		x1 = (x0*x0 + A) / (2*x0);		++iterateCount; // count iterate.		// printf("  %.15f\n", m);		if(fabs(x1 - x0) <= DBL_EPSILON) break;		if(xx == x1) return x0; // break two value cycle.		xx = x0;		x0 = x1;	}	return x1;}double SecantSqrt(double A){	double x0 = 0, x1 = A+0.25, x2;	double fx0 = x0*x0 - A, fx1 = x1*x1 - A;		for(;;) {		x2 = x1 - fx1*(x1-x0) / (fx1-fx0);		++iterateCount; // count iterate.		// printf("  %.15f\n", x2);		if(fabs(x2 - x1) < 2*DBL_EPSILON)			break;		x0 = x1; fx0 = fx1; 		x1 = x2; fx1 = x2*x2 - A;	}	return x2;}int main(){#ifdef F_INFO	puts("local machine floating point informations:");	printf("FLT_DIG: %d, %g\n", FLT_DIG, FLT_EPSILON);	printf("LDBL_DIG: %d, %g\n", DBL_DIG, DBL_EPSILON);	printf("LDBL_DIG: %d, %g\n", LDBL_DIG, LDBL_EPSILON);#endif	double x, res, stdres;		while( scanf("%lf", &x) == 1 )	{		stdres = sqrt(x);		printf("%15g ", x);				iterateCount = 0;		res = BisectionSqrt(x);		printf("%14g\t%3d\t", res-stdres, iterateCount); 				iterateCount = 0;		res = NewtonSqrt(x);		printf("%14g\t%3d\t", res-stdres, iterateCount); 				iterateCount = 0;		res = SecantSqrt(x);		printf("%14g\t%3d\t", res-stdres, iterateCount); 				printf("\n");	}		return 0;}
          
         
        
       
      

程序输出\t是为了方便重定位到文本文件后，粘贴到excel等表格软件中；格式串是为了方便控制台查看；

測试数据由以下的python脚本生成：

for x in range(1, 10000):	print x*0.01	for x in range(10000, 90000):	print x	for x in range(1000000, 9000000, 37):	print xfor x in range(100000000, 10000000000, 2311):	print x

能够通过管道进行測试：

gcc sqrt_cmp.c -o sqrt_cmp # 编译python inputgen_sqrt_cmp.py | sqrt_cmp # 測试

经过例如以下数据试验：

delta = 0.05count = 1/deltafor x in range(1, 2*int(count)):	print x*delta

得到的迭代次数随x的变化关系例如以下图所看到的：

图中，非常坐标表示x值，纵坐标表示迭代次数。

试验结果表明：牛顿法的收敛速度最快（迭代次数少），割线法次之，而二分法收敛最慢。

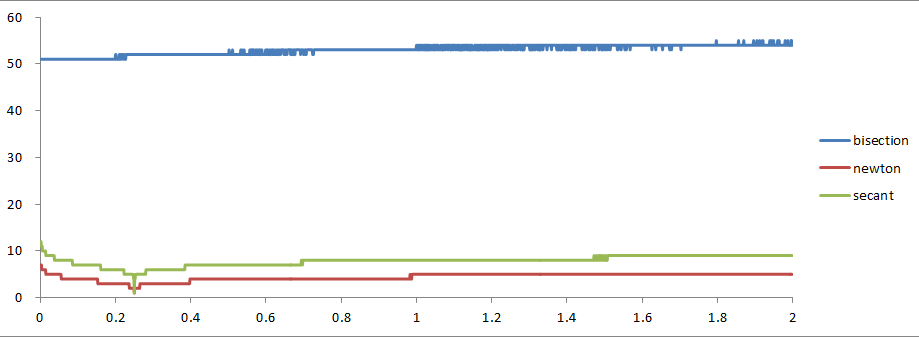
总结

本文分别描写叙述了二分法、牛顿法、割线法，等几种求方程近似解算法的步骤及实现；另外，从理论方面解释了这些算法步骤背后数学原理；并将这些方法进行了一般化的推广。最后，本文针对不同方法实现的sqrt进行了实验对照。实验结果表明：牛顿法的收敛速度快于割线法，割线法快于二分法。